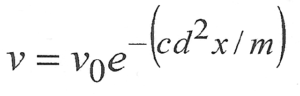Firepower of tanks in the Second World War: Historical test results compared to calculated values of the penetration power of armor-piercing shells.

Penetration power of armor-piercing shells
Table of Contents
For military War Games, conflict simulations and also in computer games, the ability of a weapon system or combat unit to penetrate a homogeneous armor-plate with the associated standard armor-piercing shell (AT), which sloped an angle of 30 degrees at a distance of 1000 meters, is used as the basis for the refraction of combat power vs armor.
Penetration Test Results
Unfortunately, the use of specific penetration values as a basis for the ability to fight tanks, results in a ‘Pandora’s Box’ being opened with respect to the ‘real’ and ‘correct’ values.
There are two main causes that lead to inaccuracies. First, there are differences between different historical sources in terms of the penetration figures obtained in tests; sometimes even for the same weapon and ammunition. Second, there are often significant differences between the actual field-tested penetration values of an armor plate and the predicted penetration values calculated with physical equations.
When looking at historical recordings of test firings, fluctuations in supposedly comparable figures are found for various reasons. These include:
The test values come from similar tests with comparable shooting distances and impact angles, but at different dates and in different countries. The armor used for the tests varies in brittleness, hardness and quality depending on the test and country, i.e. there are different Poldi or Brinell hardness values.
The definition of a ‘penetration’ varies from country to country. For example, German figures included the entire penetration, while British test numbers also allowed partial penetrations. If this is an APHE shell (armor-piercing high explosive shell), then a full penetration is required for full effect. However, if this is an AP shell, partial penetration is still effective. In particular, the British penetration figures must be treated with caution, as in some cases shots with only 20% penetrating the armor have been considered ‘penetration’.
Sometimes different propellant charges were used to determine the penetration force of a projectile. This means that the ammunition was different, even though it may have had the same designation.

Some tests also used face hardened armor, while others did not. Frontal hardened armor has more impact on an AP shell than on an APC or APCBC shell.
Taken together and retrospectively, it is not realistic to expect different tests to be identical at different times and places.
However, with careful historical research, it is possible to exclude a large part of the causes of the differences. This includes ensuring that ranges and angles are as identical as possible; ensuring the type of ammunition used; and ensuring that the definition of a penetration is reasonably consistent.
The biggest factor outside historical control seems to be the hardness and quality of the armor plates used in the test shooting. This seems to vary depending on when, where and in which country it was produced.
Nevertheless, surprisingly uniform figures emerge for the penetration values of the majority of tank and anti-tank weapons used in the Second World War.
Calculated Penetration Values
The second method is to replace the historical test values with predicted penetration values calculated using physical equations. To investigate this possibility, we consider the two basic equations used:
Pen = kmv² / d²
Where ‘Pen’ is the penetration force in mm of a vertical armor-plate (i.e. 0° degrees). ‘k’ is the coefficient that varies with the armor quality, ‘m’ is the shell mass (in kg), ‘v’ is the projectile impact velocity (in meters/sec) and ‘d’ is the shell diameter (in mm).
The change in velocity of the projectile as a function of distance is given by,
where ‘v’ is the projectile velocity (in m/s), ‘vo’ is the muzzle velocity (in m/s), ‘e’ is the exponential constant, ‘d’ is the projectile diameter (in mm), ‘m’ is the projectile mass (in kg), ‘x’ is the distance travelled by the projectile (in meters), and ‘c’ is a coefficient representing the aerodynamic resistance of the projectile. This equation assumes that the projectile’s trajectory is horizontal.
The idea behind these equations is to eliminate variations in the variables used in test firing results in order to obtain a more accurate comparison of the penetration capabilities between the different guns.
Applying these equations to some of the best known tank and anti-tank guns used during the Second World War and comparing them with historical test results leads to the results shown in the table below.
The historical test data used in this table uses the most consistent information from reputable sources. Care has been taken to ensure that uniform ranges and firing angles are used for all weapon systems considered. In addition, the selected test ammunition is of the same type, i.e. the standard AP ballistic projectile with protective cap, wherever possible.
Historical test results vs calculated values (1,000 m at 30°):
Gun | Tank (example) | Nation | Test results | Calculated values | Difference |
|---|---|---|---|---|---|
57mm M1943 (ZIS-2) L/73 (APHE or APCHE) | T-34-57, AT gun | Soviet | 85 | 100 | +32% |
90mm M3 L/51 (for 1,000 yards=914.4m) | M36 Pershing | US | 102 | 128 | +24% |
85mm ZIS-S-53 (L/54.6) | Soviet | 85 | 100 | +18% |
|
5cm KwK L/60 | German | 50 | 58 | +15% |
|
76mm M3 L/50 | AT gun | US | 82 | 92 | +13% |
57mm M1 L/50 | AT gun | US | 62 | 69 | +12% |
76.2mm F-34 L/41.5 | T-34-76 | Soviet | 49 | 54 | +11% |
7.5cm KwK 42 L/70 | German | 111 | 123 | +11% |
|
5cm KwK 38 L/42 | PzKpfw III G-J | German | 36 | 40 | +10% |
6-Pounder L/43 | Valentine, Churchill, Cromwell, AT gun | British | 71 | 77 | +8% |
17-Pounder (76.2mm) | Sherman Firefly, AT gun | British | 118 | 126 | +7% |
7.5cm KwK 40 L/48 | Pz IV, StuG III | German | 85 | 90 | +6% |
7.5cm Pak 40 L/48 | Marder, AT gun | German | 89 | 92 | +4% |
75mm M3 | Sherman 75mm | US | 60 | 61 | +2% |
76mm M1A1 L/52 | Sherman 76mm | US | 90 | 91 | +1% |
2.8cm sPzB 41 | SdKfz 221, AT gun | German | 46 | 47 | +1% |
8.8cm Pak 43/71 | Tiger II, Nashorn | German | 165 | 164 | 0% |
8.8cm Flak 18 L/56 | AT gun | German | 106 | 105 | -1% |
8-8cm Kwk36 L/56 | Tiger I | German | 100 | 98 | -2% |
3.7cm L/45 | PzKpfw III, AT gun | German | 36 | 29 | -21% |
7.5cm KwK 37 L/24 | Pz IV, StuG III | German | 35 | 25 | -27% |
In general, this table of the breakdown values shows rather unclear results, although there are probably some patterns.
In 16 out of 21 cases, the theoretical result is higher than that obtained in tests. In other words, the guns did not work as well as they theoretically should if the muzzle velocities were as indicated and the ammunition was reasonably designed and manufactured. Interestingly, all Soviet, British and American examples belong to this category, although most of them are not too far below the mark (i.e. an error rate between 1% and 10%).
For weapons with an error of 11% or more, there appears to be a fundamental problem. It is unlikely that the armor plates used by the Soviets or Western Allies were of a higher quality in the tests than those used by the Germans (which would help explain the results if this were the case), and in any case some of the German test studies also fall into this category. In these cases, the most likely (and reasonable) explanation is that the muzzle velocities were not as high as indicated, or the ammunition, construction or material was of inferior quality.

In only 5 out of 21 cases the theoretical result is lower than in the tests. These are all German test results, although most are close to the mark and within a reasonable margin of error (5% or less). The two cases with large errors (21-27%) are both weapons with relatively low muzzle velocities, i.e. the 7.5 cm KwK 37 L/24 and 3.7cm PAK 36 L/45. Again, it is unlikely that these special weapons were tested with inferior armor plates and the most likely explanation is that the muzzle velocities were actually higher than indicated.
In only one case, the theoretical result of tests is within an error rate of 0.4%. This is the German 8.8 cm Pak 43 L/71. In other words, this famous weapon was as deadly as claimed and able to destroy any tank in the world up to at least 2,000 meters.
Problems of calculations
De Marre Formula vs Krupp Formula for Penetration of Shells
Both the De Marre and Krupp formulas are historically significant equations used to calculate the penetration capability of projectiles against armor.
De Marre Formula:
The De Marre formula was created by Commandant Jacob de Marre to estimate the thickness of armor a shell will penetrate, given the penetration data of another shell. It’s commonly used in ballistic calculations for artillery shells and naval projectiles.
When using the De Marre formula, the penetration is calculated at whatever reference angle you’re using for your calculations, making it more flexible for different engagement scenarios.
Krupp Formula
The Krupp formula, in contrast, is more easy and generally suitable for low-speed projectiles to judge armor-piercing capabilities. When using the Krupp formula, penetration is calculated specifically at 90 degrees perpendicular to the armor.
Comparisons
Both formulas have been used extensively in military ballistics. The Milne version of the De Marre formula is often compared with results from the Krupp All-Purpose Armor Penetration Equation to validate findings in naval artillery research.
The De Marre formula tends to show a slightly higher increase in penetration with striking velocity compared to its Krupp counterpart, making it more suitable for higher velocity projectiles.
Coefficient for the aerodynamic resistance of the projectile
The problem with ‘c’ is that it varies with the size of the projectile, the speed at which it moves, and the aerodynamic design of the specific projectile. In general, ‘c’ remains nearly constant for projectiles moving at less than about 200 m/s. The velocity of the projectile is the same as the velocity of the specific projectile.
It rises sharply as the projectile approaches the speed of sound, for example at velocities from 200 m/s to about 350 m/s. The velocity of sound is then determined by the velocity of sound of the projectile. At velocities beyond about 350 m/s, it decreases slightly with increasing velocity.
For each gun considered in the above table, default values of ‘c’ were used to account for the variation in drag due to projectile size. In all cases – except for the German 7.5 cm KwK 37 L/24 cannon – the velocities are assumed to be over 600 m/s. The air resistance variation was calculated as a function of the projectile size. Since the variation of ‘c’ with velocity is small, the errors caused by the non-observance of ‘c’ as a function of velocity are also small.
In the table, however, ‘c’ does not take into account the aerodynamic design of the projectile warhead. This is a potentially very important source of error and difficult to calculate.
Muzzle Velocity
The second error with the introduction of the variable ‘vo’ (muzzle velocity) is much more serious than with ‘c’.
The problem is that using the above equations requires that the muzzle velocity values from the test results be entered into the equations, which of course discredits the equations !
This is a classic erroneous logic because it assumes that the muzzle velocity test fire data is correct and consistent, while the same data provided erroneous and inconsistent penetration values !
It’s a good example of old physics that says: ‘Where garbage comes in, garbage comes out’. This is especially true in this case, because the muzzle velocity was harder to measure than the actual penetration figures using World War II technology. In fact, one of the possibilities to measure the muzzle velocity was, testing the weapon to get the penetration value in a certain range and then use a physical formula to calculate the muzzle velocity !

Let us take an example from the table: the German 8.8 cm Flak 18/36. This weapon was probably the most famous artillery gun of the Second World War. The huge number of over 17,000 pieces was produced and in August 1944 10.930 Flak 18/36/37 were in service.
This weapon was probably the most extensively tested artillery gun of the Second World War: it was extensively tested by the Germans and also by the Allies, who wanted to find out everything about it.
One can well imagine, therefore, that the muzzle velocity figures for this weapon with its standard armor-piercing ammunition were fairly well-known. Well, according to some very respected sources, the 8.8 cm FlaK 18/36 L/56 and the 8.8 cm KwK 36 L/56 tank gun of the Tiger tank (a weapon directly derived from the 88 mm Flak, also firing the same armor-piercing ammunition and operating with identical ballistics) had a muzzle velocity of between 773 and 820 m/s with identical fired ammunition everywhere.
Using the above equations, at 1,000 meters against a vertical homogeneous armor-plate, this corresponds to a penetration performance of 117 mm to 132 mm.
So, using the equations and before we even consider other creeping errors, we already have a theoretical variation of the penetration power (directly derived from the different muzzle velocity values) from 98 mm to 111 mm against an armor sloped at 30°.
This difference is already greater than the original differences in penetration performance in the historical test data, which range from 100 mm to 110 mm.
In other words, when we try to determine the true penetration power of the famous Eight-Eight gun, we are actually taking a step backwards. If this is the case with one of the most frequently tested weapons of the Second World War, how can we trust the muzzle velocities of less frequently tested weapon systems more than their penetration values?

References and literature
Encyclopedia of German Tanks of World War Two (P.Chamberlain, H.L.Doyle)
Soviet Tanks and Combat Vehicles of World War Two (Steven J. Zaloga, James Grandsen)
Panzerkampfwagen des 1. und 2. Weltkrieges (Andrew Kershaw)
Fire and Movement (RAC Tank Museum)
Operation Barbarossa: the Complete Organisational and Statistical Analysis, and Military Simulation, Volume I – IIIB (Nigel Askey)