Penetrability of tank ammunition in the Second World War (Part II): Problems of calculated values for armor-piercing shells compared to the test results.


Problems with Muzzle velocity
Table of Contents
Therefore, in order to be consistent with the equations used in Part I of the World War II Tank Ammunition Penetration Test and to apply a proper scientific method, we cannot use the muzzle velocities from the same test data where we are trying to replace the penetration figures of the shells.
We would therefore have to calculate the muzzle velocity for each weapon system !
One could initially be of the opinion that the calculation of the muzzle velocity is a relatively simple matter. To do this, the pressure inside the breech chamber must be determined and the acceleration of the projectile must be calculated over the length of the barrel. These are the dominating factors which determine the muzzle velocity and give an approximate value.
However, the breech chamber pressure values are only available for some weapons and these are not more reliable or consistent than muzzle velocity or direct penetration measurements. In order to accurately calculate the muzzle velocity, where plus or minus 1% must not be exceeded, the following should be considered:
Knowledge of the chemical composition of the propellant and chemical combustion efficiency, ammunition design and amount of propellant used, the significant variations in the force behind the projectile (the force on the projectile changes as it is accelerated along the barrel by the increase in chamber volume and expanding gases), the friction in the barrel, exact projectile mass, exact barrel length, gun breach and barrel tolerances at the production (e.g. the greater the tolerances, the more gases escape at the sides of the projectile, which can drastically reduce the muzzle velocity and increase the instability of the projectile) and the effects of the barrel rifling (this determines the rotation of the projectile, which affects the forces on the projectile and its acceleration time).
This matter is much more complex and problematic than the actual calculation of the penetration figures !
Even with the best available information and computer power, our calculated muzzle velocities and the resulting calculated penetration value will never be more accurate or consistent than the data from direct historical test results.
Error in Muzzle Velocity data
The table provides further evidence that some stated muzzle velocities must be inaccurate.
As already mentioned, the muzzle velocity is largely dependent on the ratio of propellant, projectile mass and barrel length. It is interesting to note that for some weapons of similar caliber, the stated muzzle velocity is higher, although the respective weapon has a shorter caliber barrel length than comparable weapons.
Historical test results vs calculated values (1,000 m at 30°):
Gun | Tank (example) | Nation | Test results | Calculated values | Difference |
|---|---|---|---|---|---|
57mm M1943 (ZIS-2) L/73 (APHE or APCHE) | T-34-57, AT gun | Soviet | 85 | 100 | +32% |
90mm M3 L/51 (for 1,000 yards=914.4m) | M36 Pershing | US | 102 | 128 | +24% |
85mm ZIS-S-53 (L/54.6) | Soviet | 85 | 100 | +18% |
|
5cm KwK L/60 | PzKpfw III J | German | 50 | 58 | +15% |
76mm M3 L/50 | AT gun | US | 82 | 92 | +13% |
57mm M1 L/50 | AT gun | US | 62 | 69 | +12% |
76.2mm F-34 L/41.5 | T-34-76 | Soviet | 49 | 54 | +11% |
7.5cm KwK 42 L/70 | Panther | German | 111 | 123 | +11% |
5cm KwK 38 L/42 | PzKpfw III G-J | German | 36 | 40 | +10% |
6-Pounder L/43 | Valentine, Churchill, Cromwell, AT gun | British | 71 | 77 | +8% |
17-Pounder (76.2mm) | Sherman Firefly, AT gun | British | 118 | 126 | +7% |
7.5cm KwK 40 L/48 | Pz IV, StuG III | German | 85 | 90 | +6% |
7.5cm Pak 40 L/48 | Marder, AT gun | German | 89 | 92 | +4% |
75mm M3 | Sherman 75mm | US | 60 | 61 | +2% |
76mm M1A1 L/52 | Sherman 76mm | US | 90 | 91 | +1% |
2.8cm sPzB 41 | SdKfz 221, AT gun | German | 46 | 47 | +1% |
8.8cm Pak 43/71 | Tiger II, Nashorn | German | 165 | 164 | 0% |
8.8cm Flak 18 L/56 | AT gun | German | 106 | 105 | -1% |
8-8cm Kwk36 L/56 | Tiger I | German | 100 | 98 | -2% |
3.7cm L/45 | PzKpfw III, AT gun | German | 36 | 29 | -21% |
7.5cm KwK 37 L/24 | Pz IV, StuG III | German | 35 | 25 | -27% |
In this case, the additional muzzle velocity can only be attributed to the quantity and quality of the propellant used in the shell. If the actual penetration values for the weapons with shorter barrels are about 20% below the expected theoretical penetration force and the ratio of propellant to projectile mass is comparable to that of other guns in the class, this serious evidence suggests that the deviation is more due to an incorrectly reported muzzle velocity than to mysteriously hard armor plates in the firing tests.
This is all the more true if the combat reports are based on the test results and the respective country has a mixed record in the production of high-quality armor plates.

Examples from the table are the US 90mm M3 L/51 and the Soviet 85mm ZiS-S-53 L/54.6. Both guns are shorter than the 8.8 cm KwK 36 L/56 of the Tiger I in their actual and caliber-related length, have a similar propellant and projectile mass ratio and should nevertheless have higher muzzle velocities.
The worse test values for the Allied guns cannot simply be attributed to the German tests with poor test armor or their obvious inability to measure 1,000 meters and an angle of 30 degrees. It is much more likely that the muzzle velocities are overrated and the ammunition was of inferior design and quality.
Another indirect evidence of suspicious muzzle velocities stems from the relatively rare cases in which the historical test result is significantly higher (i.e. about 20% or more) than the theoretically calculated penetration values.
Fluctuations of a few percent may easily be due to different qualities of the armor plates or deviations in the test procedure, but such a positive excursion of this magnitude leads to at least one of the underlying parameters or assumptions being incorrect.
The most likely is an underestimated muzzle velocity, as it is very unlikely that the ammunition performance of standard armor-piercing projectiles would increase the penetration to such an extent.
An example from the table is the German 7.5-cm KwK 37 L/24.
The penetration rates in the tests of this weapon are very consistent between the sources and show that the actual penetration is about 27% higher than the calculated values. This even requires a very generous downward angle of 15 degrees on impact to take into account the low muzzle velocity and relatively high trajectory of this weapon (i.e. a 15 degree impact angle is used in the calculation and not 30 degrees).
A variation of this magnitude is most likely not solely due to variations in test procedure or armor quality, while an increase of only 17% (i.e. an additional 67 m/s) in muzzle velocity estimation compensates for the difference between theory and practice.
Design of ammunition
The equations
Pen = kmv² / d²
and
do not take into account variations in ammunition design or the manufacturing quality of standard armor piercing shells between particular guns or between different nations.
Two basic assumptions are that projectiles of the same caliber (diameter) differ only in their mass and that all projectiles are identical, made of a solid piece of homogeneous metal.
These are rather far-fetched assumptions, because it is very likely that two guns of the same caliber with the same muzzle velocity and ammunition (e.g. APCBC armor-piercing high explosive shell) will have different penetration values solely due to the design and manufacturing quality of the respective weapon !
The ammunition for a weapon has usually been developed as carefully as the weapon itself, since it is part of the weapon system and cannot be separated from it. This applies in particular to anti-tank weapons and the associated range of the armor-piercing AP projectiles.
If the design of ammunition and manufacturing quality is ignored, the technology used in the development of the guns is also ignored, and thus a good part of the overall weapon system.
Many good guns failed or were at least severely limited in their effectiveness because the ammunition was defective or poorly constructed. An armor-piercing round ballistic cap shell (APCBC), especially with a highly explosive filler, is not simply a piece of homogeneous metal moving at high-speed. Even the design and selection of materials for relatively simple and solid AP armor-piercing shell poses a challenge.
Before the projectile even hits the armor, the ballistic shape influences the penetration. The shape of the shell has a direct influence on the value ‘c’ in the equations. Projectiles without a ballistic cap and instead of a much duller armor-piercing cap have a much greater speed reduction due to the higher drag, especially over greater distances.
For similar shells with ballistic caps the individual ballistic design of the caps has to be considered. After impact, the ballistic cap breaks so that the armor-piercing cap can come into contact with the armor, and different designs of armor-piercing caps also have different effects on the armor.
A well-designed armor-piercing cap not only supports penetration into face-hardened armor, but also improves performance at oblique angles of impact. Even though the ballistic and armor-piercing caps are identical, projectiles from different guns have a complex and different internal structure and are made of different high quality materials.

Clear indirect indications of the influence of the size of the ammunition on the armor can be found in the table above. It seems that the deviation between the actual and calculated penetration tends to increase with decreasing caliber. In addition, in all 13 cases where the weapon has 76.2 mm caliber or less and the impact velocity is greater than 647 m/s (i.e. supersonic velocities), the actual penetration during test firing is less than the theoretically calculated value. For anti-tank weapons in calibers from 57 mm to 50 mm, the deviation between actual and calculated penetration can even be up to 32%. This would mean that something fundamental has happened.
If all the projectiles of the weapons in the table are made of similar material, it seems that smaller projectiles moving at supersonic velocities are much less able to withstand the impact on an armor plate without breaking, as opposed to larger projectiles moving at similar velocities.
It is interesting to note that the 50mm to 57mm anti-tank guns became much more effective when they were used with various types of ‘special’ hard core ammunition. The low ability of smaller shells to remain intact to allow at least partial penetration of an armor-plate compared to larger cannons, even though they have the same kinetic energy when fired, is one of the two main reasons why most armed forces switched to larger anti-tank guns during World War II and did not simply build lighter and long-barreled 50 mm to 57 mm weapons.
The equations take into account the increased ability of smaller caliber guns to penetrate due to the smaller surface area at impact, i.e. the smaller shells have less armor to break out of their trajectory.
However, the equations do not take into account the tendency of smaller shells to break before the armor has penetrated.
This has to be considered before we consider additional effects of the design of the ammunition of the respective weapon.
The American 90 mm M3 L/51 cannon from the table above can serve as an example for the possible influence of the specific design of the ammunition and its manufacturing quality on the penetration force on armor plates.
The very large deviation between the test results and the calculated value is not easily discarded even with inconsistent armor quality or non-identical test procedures. Various reports direct from the US Army lead to the following conclusion: ‘The 90mm M3 shell fired by the M36 tank destroyer and the M26 Pershing heavy tank weighed twenty-four pounds and had more impact than the German 88 mm shell fired from the Tiger I’s weapon. Since the quality of the steel used for the ammunition construction, however, was worse than that of the Germans, the penetration performance compared to the German grenade remained far behind expectations‘.
Conclusions historical test results vs calculated values of penetration figures
On its own, it is difficult to draw direct conclusions from the data presented in the table. However, given the physical laws and experiences of the Second World War and the above explanations, there are some general conclusions that can be drawn.
There is no doubt that there are inconsistencies and variations in supposedly identical data from test shots and the reasons for these deviations are the quality of the armor plates and, to a lesser extent, the different test methods.
It is a fundamental failure of the scientific method to assume that the test data for muzzle velocity are correct or at least consistent, while the same data are said to have provided false or inconsistent data about the penetration. In addition, accurate muzzle velocity calculations can only be performed with potential sources of error.
The equations do not fully take into account the often dramatic effect of the ammunition design of a particular weapon system or the quality of the material used in its construction. Thus, comparable types of ammunition, such as armor-piercing ballistic cap (APCBC) ammunition, have a wide range of design and manufacturing quality factors that influence the performance of an armor penetration.
The equations do not take into account the fact that smaller projectiles of the same material, which have similar kinetic energy on impact, have a higher tendency to fracture before the impact on the armor-plate occurs – compared to larger shells.
In summary, the equations have little ability to accurately calculate the complexity of ammunition design and manufacturing quality for the armor penetration, realistic and accurate muzzle velocities or weapon tolerances.
On the other hand, the historical test data, despite their inconsistencies, used the actually built weapons and projectiles to obtain the penetration values. The shells used and the tolerances in the manufacture of the cannons were thus treated as part of the overall weapon system – and it is this actually functioning weapon system that is interesting for the result.
In physics, the historical test data is still the only available link between the world of theoretical and experimental physics.
In the end, it is still more accurate to rely on actual shooting data to get the most realistic picture possible of the ‘true’ relative penetration force.
However, it is important to ensure that consistent test parameters are used as far as possible by referring to this data from as many alternative sources as possible. This is the only way to consider the overall design of the weapon, the design of the ammunition and the manufacturing quality and tolerances of the entire weapon system.
References and literature
Encyclopedia of German Tanks of World War Two (P.Chamberlain, H.L.Doyle)
Soviet Tanks and Combat Vehicles of World War Two (Steven J. Zaloga, James Grandsen)
Panzerkampfwagen des 1. und 2. Weltkrieges (Andrew Kershaw)
Fire and Movement (RAC Tank Museum)
Operation Barbarossa: the Complete Organisational and Statistical Analysis, and Military Simulation, Volume I – IIIB (Nigel Askey)





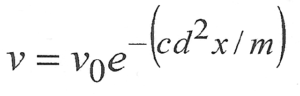





Your penetration formula is “provably lame”.
Assuming the same materials, if you will double size of projectile you should get double penetrated armor value. It is simple observational and logical fact.
Your formula can not reproduce this, gives totally wrong scaling and that’s why you get systematic error. You should use de Marre formula – it is the most accurate among simple ones, and perfectly matches observed penetration curves, recreates scaling “double projectile size = double penetration”.
Actually, materials can withstand stronger forces when force is applied in shorter times. Hence, bigger projectiles that penetrates longer in time have small bonus that comes directly from that penetration time.
That’s why de Marre use additional correction factor on the top of sane physical assumptions (for example it doesn’t matter if kinetic energy comes from mass or velocity)
De Marre (from the beginning of the 1800s) is in some cases a bit better than Krupp (a few mm), but there is still often a huge difference to test values of many guns, since the velocity calculation (which couldn’t be tested at these times) of the guns is often much more inaccurate, as the article points out.
So, overall, it’s much better to rely on the test values for the penetration of the guns and not on some formulas.
A couple of points:
1. The penetration equation used is equivalent to Morin’s formula. As far as I can make out this has never been a popular formula for the calculation of official penetration tables. I believe that the Germans would be more likely to use a Krupp formula, or Tierberg’s, the British Milne, the Americans de Marre, and the Russians the K2400 formula (equivalent to Krupp).
2. The standard of proof plate may well have varied between nations; the British changed their proof plate standards several times during the war.
3. The criteria used for penetration also vary, and can produce substantial variation in results.
4. It is often not easy (even with access to official range tables) to find reliable information on the way velocity decays with range. Obviously striking velocity has a considerable influence on penetration performance. I would very much like to know what values you used for c in the velocity decay equation, and where you got them from.
All the best,
John.